
vers l'index général de l'aide
vers les lathes
Fichiers de générateurs de splines
Utilisez le fichier lathe_demo.pov pour faire des essais comme dans les exemples !
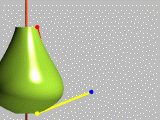
Linear_spline
la courbe suit les points et forme une ligne brisée.
exemple : <12,40>,<08,30>,<19,25>,<22,15>,<15,05>,<00,00>
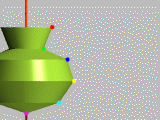
quadratic_spline
Dans l'intervalle entre deux points, la position du point précédent détermine l'inclinaison de
la courbe jusqu'au point suivant. La position du troisième point n'est pas prise en compte.
Si les quadratiques paraissent plus lisses que les linéaires, en général, au point de transition,
ce n'est pas le cas, car l'inclinaison (la pente de la fonction, pour les matheux) n'est pas la
même de chaque côté du point.
exemple : <35,40>,<08,38>,<09,25>,<22,15>,<15,05>,<00,00>
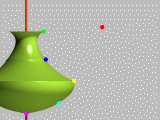
cubic_spline
Avec les cubiques le problème des transitions est résolu. Le troisième point étant un point de
contrôle, les courbes sont parfaitement continues, même aux points de transition.
exemple : <35,30>,<08,38>,<05,30>,<22,15>,<08,00>,<30,00>
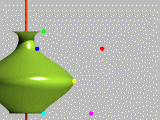
Une bezier_spline est une courbe dont les segments sont définis par
deux extrémités et deux tangentes (les tangentes de la courbe à chacune des extrémités).
Une bezier_spline est donc définie par un ensemble de points groupés
par quatre. Pour chaque segment de la courbe, les points 1 et 4 sont les extrémités,
et les points 2 et 3 les points de controle (la tangente au point 1 est le segment de droite
entre les points 1 et 2, et celle au point 4 est la droite entre 3 et 4). On peut bien entendu
utiliser autant de segments de 4 points qu'on le souhaite, mais on a généralement intérêt
à faire en sorte que les segments se joignent (point 4 = point 5,..).
exemple : <05,40>,<10,20>,<30,10>,<05,00>
exemple : <05,40>,<20,25>,<30,10>,<05,00>

|
 |
Le nombre de points par courbe dépend du type de spline. Pour les linear_spline nous aurons n-1 segments. Pour une quadratic_spline le nombre de segments est égale à n-2 car le dernier point est utilisé pour l'inclinaison, (il faudra au moins trois points pour une quadratique). Pour une cubique_spline c'est n-3 segments avec le premier et dernier servant à l'inclinaison (il faudra au moins quatre points). la bezier_spline demande un multiple de quatre points .
Les problèmes liés à la fermeture éventuelle de la courbe génératrice sont les mêmes qu'avec les prismes. Reportez-vous à la page qui explique les splines appliquées aux prismes pour une explication détaillée.
Rédacteur : Martial Rameaux
vers les Lathes
vers l'index général de l'aide