vers l'index général de l'aide
vers la page des bicubic_patch

approximation des primitives avec des surfaces bézier

objectif

Créer des surfaces coniques, sphériques, cylindriques ou toroïdales avec des surfaces bézier.

compatibilité

POV-Ray 2.0 +sup.

syntaxe

La syntaxe est telle que décrite à la première page sur les patches bicubiques, cette page ne concerne que le choix des points de contrôle qui produira telle ou telle surface.

Peut-être un petit avant-garde: les surfaces bézier ne reproduisent pas exactement les primitives mentionnées ci-haut, par contre la différence est négligeable, l'erreur maximale atteignant environ 0,7%, qui est tout à fait acceptable, à moins que l'on fasse des calculs portant sur l'astronomie, et le cas échéant, vous serez prévenus!

Pour approximer les primitives, il nous faut deux choses: les points de contrôle d'un quart de cercle, et les points pour une ligne droite. Toutes les primitives ont des coupes transversales qui sont soit droites ou circulaires. Il suffira donc de fournir des points qui produiront des lignes et des quarts de cercle, en combinaisons appropriées, pour obtenir les primitives.

Les points qui donnent une ligne droite: la solution est triviale, quatre points colinéaires.

Quant au quart de cercle, examinons la figure ci-dessous.

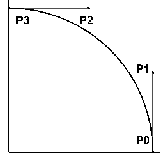
P0 et P1 sont colinéaires et à x = R. De façon semblable, P2 et P3 sont colinéaires, à z = R. Le seul inconnu est la position en z de P1 (la position en x de P2 est la même que cette dernière par symmétrie).

Comment trouver l'inconnu? En calculant un point connu sur la courbe.

P(u) = B0(u)*P0 + B1(u)*P1 + B2(u)*P2 + B3(u)*P3

où Bi(u) est le polynôme Bézier pour le point i. Ils sont:

B0(u) = (1-u)^3

B1(u) = 3*u*(1-u)^2

B2(u) = 3*u^2*(1-u)

B3(u) = u^3

Appliquant la formule pour le point au milieu de la courbe (u = ½), x = z = sqrt(2)/2. Ceci mène à z1 = x2 = 4/3*(sqrt(2)-1)*R

Nommons FBEZ le facteur du rayon R

Le cylindre

Les points de contrôle seront les mêmes, sauf que leur composante y sera différente pour chaque série de quatre points: (hauteur H)

    <R, 0, 0>, <R, 0, R*FBEZ>, <R*FBEZ, 0, R>, <0, 0, R>,
    <R, 1/3*H, 0>, <R, 1/3*H, R*FBEZ>, <R*FBEZ, 1/3*H, R>, <0, 1/3*H, R>,
    <R, 2/3*H, 0>, <R, 2/3*H, R*FBEZ>, <R*FBEZ, 2/3*H, R>, <0, 2/3*H, R>,
    <R, H, 0>, <R, H, R*FBEZ>, <R*FBEZ, H, R>, <0, H, R>

Le cône

Le rayon du cône diminue proportionnellement avec sa hauteur, donc il suffit de multiplier les composantes x et z des deuxième et troisième lignes par 2/3 et 1/3, respectivement. Les quatre points de la dernière ligne sont coïncidents à <0, H, 0>

La sphère

Les choses commencent à se corser! Quant à la sphère, il faut visualiser les mêmes quatre points de contrôles "élémentaires" mais dans les trois dimensions.

    <R, 0, 0>, <R, 0, R*FBEZ>, <R*FBEZ, 0, R>, <0, 0, R>,
    <R, R*FBEZ, 0>, <R, R*FBEZ, R*FBEZ>, <R*FBEZ,R*FBEZ, R>, <0, R*FBEZ, R>,
    <R*FBEZ, R, 0>, <R*FBEZ, R*FBEZ, R*FBEZ^2>, <R*FBEZ^2, R, R*FBEZ>, <0, R, R*FBEZ>,
    <0, R, 0>, <0, R, 0>, <0, R, 0>, <0, R, 0>

Le tore

Finalement pour le tore, il faudra 2 patches bézier, une pour une partie de l'extérieur et une autre pour l'intérieur. En plus, le facteur BEZ sera appliqué parfois au rayon majeur, parfois le rayon mineur, ou encore leur somme ou leur différence. Le code suivant produira les deux parties:

//tore - section extérieure
#declare P[0] = <R1+R2,0,0>;
#declare P[1] = <R1+R2,0,BEZ*(R1+R2)>;
#declare P[2] = <BEZ*(R1+R2),0,R1+R2>;
#declare P[3] = <0,0,R1+R2>;;

#declare P[4] = <R1+R2,R2*BEZ,0>;
#declare P[5] = <R1+R2,R2*BEZ,(R1+R2)*BEZ>;
#declare P[6] = <(R1+R2)*BEZ,R2*BEZ,R1+R2>;
#declare P[7] = <0,R2*BEZ,R1+R2>;

#declare P[8] = <R1+R2*BEZ,R2,0>;
#declare P[9] = <R1+R2*BEZ,R2,BEZ*(R1+R2*BEZ)>;
#declare P[10] = <BEZ*(R1+R2*BEZ),R2,R1+R2*BEZ>;
#declare P[11] = <0,R2,R1+R2*BEZ>;

#declare P[12] = <R1,R2,0>;
#declare P[13] = <R1,R2,R1*BEZ>;
#declare P[14] = <R1*BEZ,R2,R1>;
#declare P[15] = <0,R2,R1>;
//insérer le code pour invoquer la surface bézier avec les points P[0]-P[15]
//section intérieure
#declare P[0] = <R1-R2,0,0>;
#declare P[1] = <R1-R2,0,BEZ*(R1-R2)>;
#declare P[2] = <BEZ*(R1-R2),0,R1-R2>;
#declare P[3] = <0,0,R1-R2>;

#declare P[4] = <R1-R2,R2*BEZ,0>;
#declare P[5] = <R1-R2,R2*BEZ,(R1-R2)*BEZ>;
#declare P[6] = <(R1-R2)*BEZ,R2*BEZ,R1-R2>;
#declare P[7] = <0,R2*BEZ,R1-R2>;

#declare P[8] = <R1-R2*BEZ,R2,0>;
#declare P[9] = <R1-R2*BEZ,R2,BEZ*(R1-R2*BEZ)>;
#declare P[10] = <BEZ*(R1-R2*BEZ),R2,R1-R2*BEZ>;
#declare P[11] = <0,R2,R1-R2*BEZ>;

#declare P[12] = <R1,R2,0>;
#declare P[13] = <R1,R2,R1*BEZ>;
#declare P[14] = <R1*BEZ,R2,R1>;
#declare P[15] = <0,R2,R1>;
//insérer le code pour invoquer la surface bézier avec les points P[0]-P[15]

Rédacteur: Serge Larocque (Libellule)